Você sabe o que é fator de potência ?
Neste artigo, vamos explicar o que é, como calcular e como corrigir o fator de potência em uma instalação elétrica.
Você vai aprender também, o que é potência ativa, reativa, aparente, e qual a relação com o fator de potência.
Portanto, se você quer aprender mais sobre esse assunto, então, continue lendo esse artigo.
Mas antes de ler este artigo completo, você precisa baixar agora o Novo Kit 64 eBooks para Eletricistas e Engenheiros, confira.
Clique no botão abaixo para conhecer todos os 64 eBooks e baixar agora.
Não deixe para depois, porque todos os eBooks juntos podem não estar disponíveis em breve, então acesse o botão verde acima para saber mais e baixar todos os eBooks hoje mesmo.
O que é fator de potência
O fator de potência é a relação entre potência ativa e a potência reativa, que indica a eficiência com a qual a energia está sendo usada.
Essa eficiência é medida pela razão entre a potência ativa e a potência aparente, que indica quanto da potência elétrica consumida está de fato sendo convertida em trabalho útil (Kw).
Essa relação entre a potência ativa e aparente, pode indicar um valor baixo ou alto de fator de potência, numa escala compreendida entre 0 até 1.
Mas, para que possamos compreender o fator de potência, é necessário entender o conceito de potência ativa, potência reativa e potência aparente.
Por isso, vamos conhecer agora os três tipos de potência de circuitos elétricos em sistemas alternados.
Potência ativa
É a potência que efetivamente realiza trabalho gerando calor, luz, movimento, e faz os motores girarem, realizando o trabalho do dia a dia.
A unidade de medida da potência ativa é o Watts (W) ou Kilowatts (KW), e sua simbologia é representada pela letra maiúscula P.
Potência reativa
É a potência usada apenas para criar e manter os campos eletromagnéticos, necessário para que o eixo dos motores possam girar.
A potência reativa está presente em motores, transformadores, reatores, lâmpadas fluorescentes, etc.
A potência reativa não produz trabalho útil, mas circula entre o gerador e a carga, exigindo do gerador e do sistema de distribuição uma corrente elétrica adicional.
A potência reativa é medida em kilovolts Amperes Reativos (KVAr), e sua simbologia é representada pela letra maiúscula Q.
Potência aparente
A potência aparente é a potência total absorvida por uma instalação elétrica.
Se efetuarmos a composição da potência ativa e a potência reativa, achamos a potência aparente ou total.
A potência aparente é medida em kilovolts-amperes (KVA), e sua simbologia é representada pela letra maiúscula S.
Para que você possa entender melhor, vou fazer uma comparação bem didática entre os tipos de potência e um copo de cerveja.
Relação entre os tipos de potências
Quando você pede um copo de chopp, o ideal seria se viesse cheio de líquido até a borda, mas geralmente temos uma camada de espuma no topo.
Na imagem acima, coloquei o copo cheio de chopp com as representações de carga das potências, com as setas de limitação.
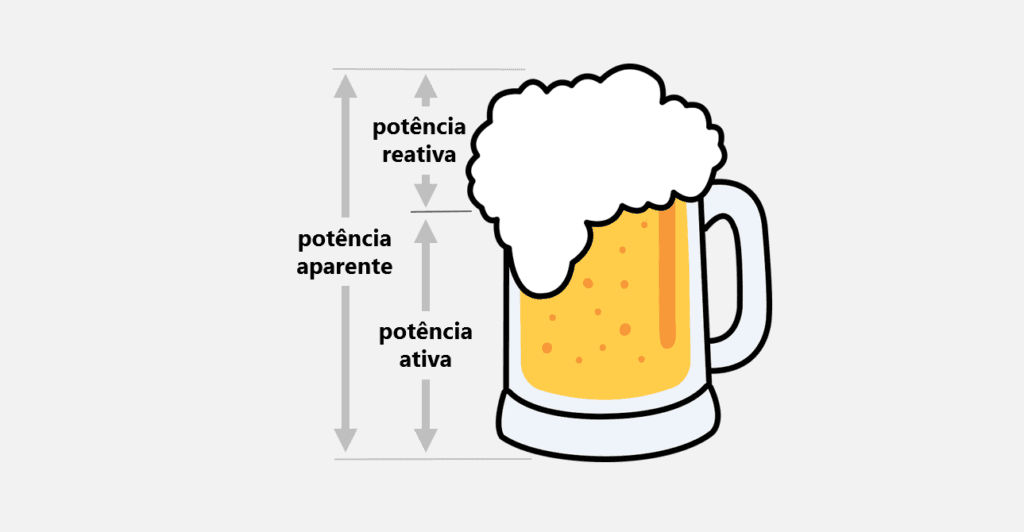
Perceba que, a camada de espuma que apesar de não ter sido comprada, ocupa lugar no copo que poderia estar cheio de chopp.
Neste caso, o copo todo representa a potência aparente (VA), o chopp líquido a potência ativa (W), e a espuma (indesejada) a potência reativa (VAr).
Espero que você tenha entendido este exemplo sobre o fator de potência e os tipos de potências envolvidas.
Nosso próximo passo agora é aprender a calcular o fator de potência, vamos lá!
Como calcular o fator de potência
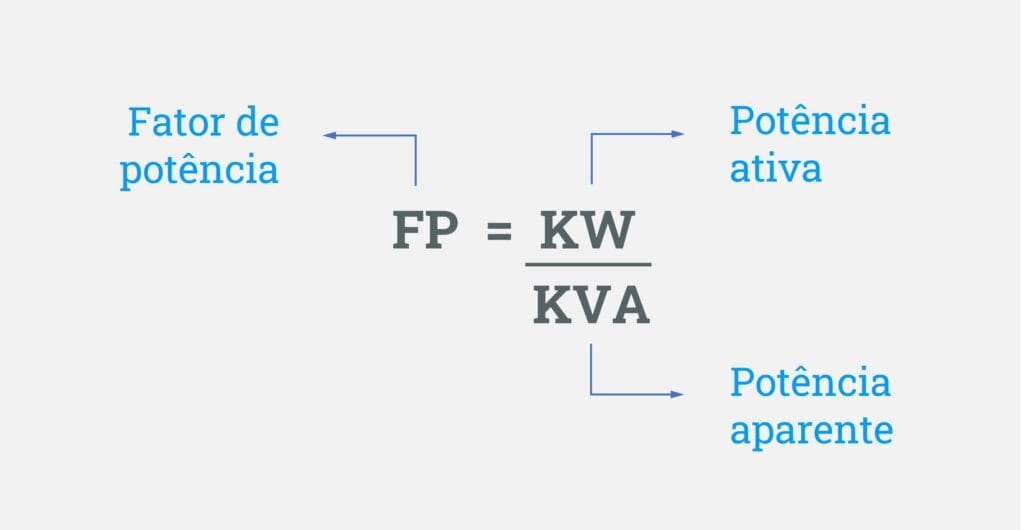
No início deste artigo, nós dizemos que o fator de potência (FP), é a razão entre a potência de ativa (KW) e a potência aparente (KVA).
Observando a analogia que fizemos acima da caneca de cerveja, podemos concluir que o fator de potência seria a relação entre cerveja ( KW ) e cerveja mais espuma ( KVA ), confira agora um exemplo prático.
Exemplo prático
Para ficar mais fácil a interpretação, vamos usar um exemplo didático simples do cálculo do fator de potência.
Supondo que tenhamos um sistema com uma potência aparente de 100 VA e esse sistema esteja consumindo uma potência ativa de 80 W.
Neste exemplo didático, qual seria o fator de potência desse sistema? Para facilitar o entendimento fiz o cálculo na imagem abaixo, veja!
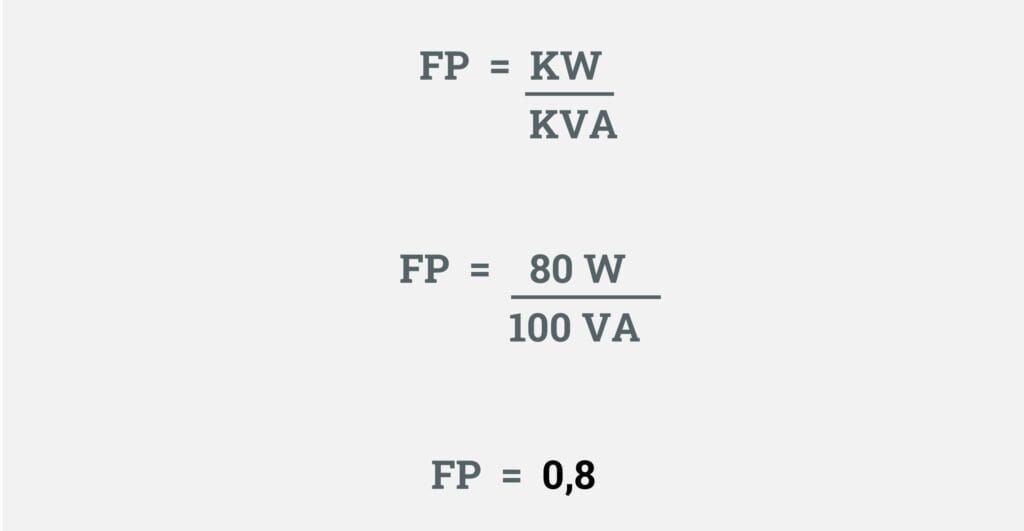
Utilizando a fórmula, fiz a substituição dos valores da potência ativa e potência aparente, logo após a divisão, encontramos o fator de potência no valor de 0,8.
Isso significa que de toda a minha potência que está chegando no meu sistema, apenas 80% está sendo convertida de fato em trabalho útil.
Conclusão
Analisando de maneira geral, este exemplo e o exemplo da caneca de choop, podemos concluir que:
Quanto maior a quantidade de espuma no copo, (quanto maior a porcentagem de KVAR), menor será sua proporção de KW ( cerveja ) para KVA ( cerveja mais espuma ).
Ou seja, com o aumento de potência reativa, haverá menos potência ativa, gerando uma redução do fator de potência.
Porém, quanto menos espuma você tiver no copo ( quanto menor a porcentagem de KVAR ), maior será sua proporção de KW ( cerveja ) para KVA ( cerveja mais espuma ).
Isso significa que a medida que a potência reativa diminui (KVAR) ou se aproxima de 0, haverá mais potência ativa, gerando um aumento do fator de potência, mais próximo de 1.
Observação importante
A analogia da caneca de cerveja que nós usamos como exemplo ainda é um pouco simplista.
Na realidade, quando calculamos a potência aparente (KVA), devemos determinar a “ soma vetorial ” da potência ativa (KW) com a potência reativa (KVAR).
Uma maneira de facilitar o processo de cálculo das potências e do fator de potência é transformá-la em um triângulo retângulo.
Portanto, devemos ir um passo além e observar o ângulo entre esses vetores, vamos lá!
Triângulo das potências
O triângulo de potências reflete a relação entre as três componentes da potência elétrica, a potência ativa, reativa e aparente.
Na imagem abaixo, fizemos o desenho de um triângulo retângulo para representar a relação entre as potências e o fator de potência.
Sabemos que em um triângulo retângulo temos dois lados iguais sendo o cateto oposto, cateto adjacente e a hipotenusa.
Exemplo do triângulo das potencias
Nossa representação ficou da seguinte forma, o cateto adjacente é a potência ativa (kW), o cateto oposto ao ângulo é a potência reativa (kvar), e a hipotenusa é a potência aparente (kVA).
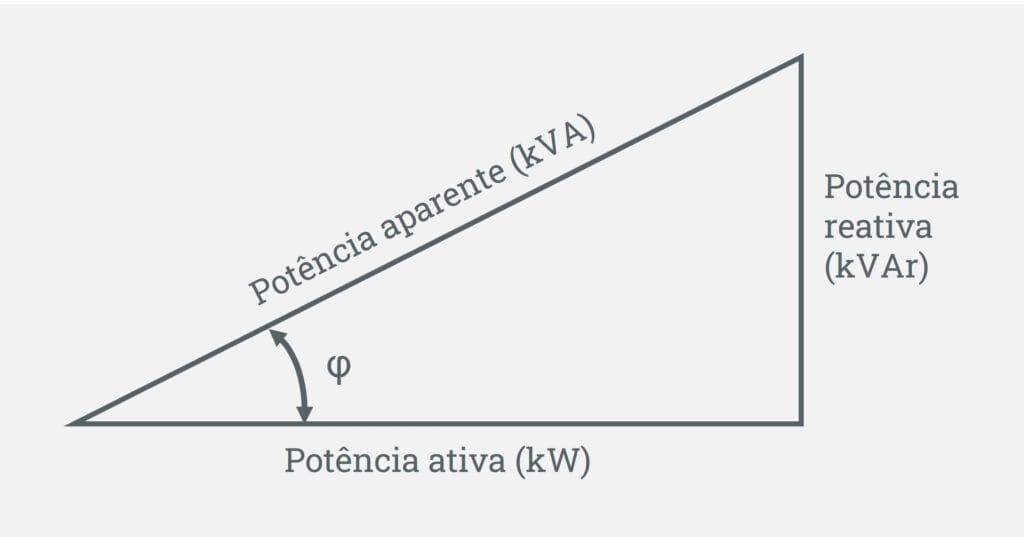
Perceba que, a potência ativa e a potência aparente formam o lado adjacente e hipotenusa do triângulo retângulo.
Fórmula para descobrir o ângulo do fator de potencia
Observe na imagem, que existe uma relação determinada pelo cosseno do ângulo entre a potência ativa e a aparente.
Ou seja, esse ângulo é gerado pelo cosseno do ângulo de fase, entre a potência ativa e a potência aparente, representado pelo ângulo φ.
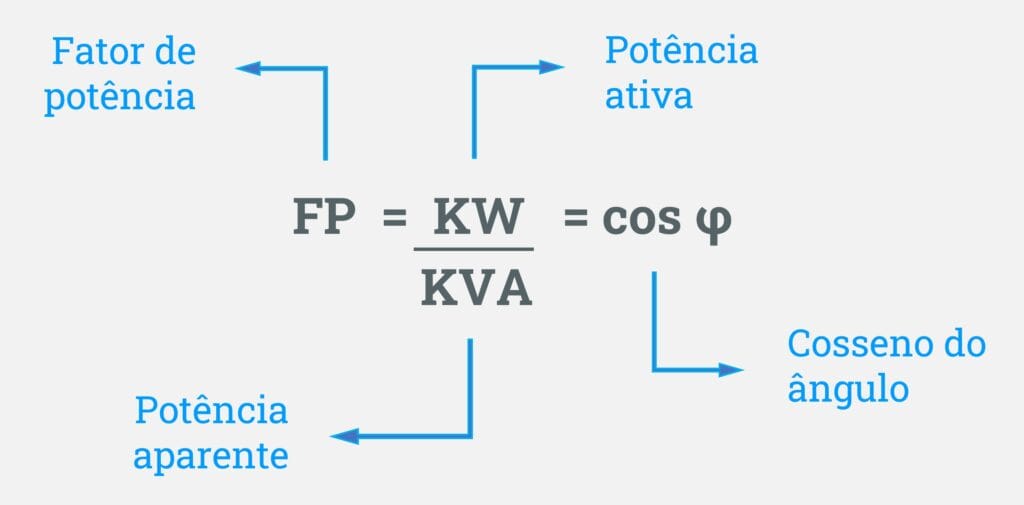
Observando a imagem acima, podemos ver que o fator de potência pode ser calculado com base no ângulo fase ou na relação entre a potência ativa e a potência aparente.
Para conseguirmos chegar neste resultado, vamos levar em consideração a redução do ângulo gerado, este ângulo é representado pela letra fi.
Consideramos sempre o cosseno desse ângulo, teremos então que considerar o cosseno de fi.
No exemplo que eu citei acima, encontramos o fator de potência de 0.8.
Neste caso, se calcularmos o inverso do cosseno (cos-1) de 0,8, encontraremos o ângulo de 36,86 graus.
Quando aplicar o fator de potência
O fator de potência é utilizado tanto em residências ou indústrias, porém sua atenção maior ganha destaque na indústria devido a atuação de vários equipamentos indutivos.
Vou começar falando sobre a importância do fator de potência na elaboração de projetos elétricos residenciais.
Se você tem mais interesse em saber como o fator de potência é usado na indústria, clique aqui para ir direto ao assunto.
Iluminação e tomadas
Em projetos elétricos residenciais e prediais, quando deseja se saber quanto de potência aparente foi transformada em potência ativa, aplica se os seguintes valores de fator de potência.
Para projetos elétricos residenciais é comum os seguintes valores utilizados abaixo.
Apesar de ser tipicamente usado por vários projetistas, esse dado pode variar conforme a concessionária local.
Por exemplo, em Minas Gerais a concessionária local é a Cemig, e a norma técnica para instalações elétricas residenciais é ND 5.1.
Neste caso a Cemig, traz 3 recomendações abaixo, veja:
- É recomendável que a previsão de cargas de iluminação e o número de tomadas, feita pelo consumidor, atenda as prescrições da NBR 5410.
- Para lâmpadas incandescentes, considerar : kVA = kW ( fator de potência unitário).
- Para lâmpadas de descarga ( vapor de mercúrio, sódio e fluorescente ) e tomada considerar : kVA = kW / 0,92.
Neste caso a Cemig está considerando um fator de potência de 0,92, e não 0,80, para tomadas e lâmpadas de descarga.
Por isso, é sempre recomendável consultar a norma da concessionária local e verificar essas informações.
Mas o que acontece no caso das tomadas de uso específicas, podemos aplicar o mesmo critério?
Tomadas de uso específicas
Neste caso, a carga a considerar para um equipamento de utilização é a potência nominal por ele absorvida.
Essa carga a considerar, é dada pelo fabricante ou calculada a partir da tensão nominal, da corrente elétrica e do fator de potência.
Nos casos em que for dada a potência nominal fornecida pelo equipamento (potência de saída), e não a absorvida, devem ser considerados o rendimento e o fator de potência.
Para ficar mais fácil o entendimento e aplicação do fator de potência, preparamos um exemplo abaixo.
O exemplo que vamos abordar, é parte de um artigo que já fizemos ensinando como fazer a divisão de circuitos elétricos em uma residência.
Se você ainda não sabe como atribuir as potências conforme a norma NBR 5410, recomendo a leitura e tirar suas dúvidas que pode vir a surgir, então vamos lá.
Para ficar mais fácil, nossa tabela de previsão de cargas está com todas as dependências, e as potências calculadas conforme a norma NBR 5410.
Veja que no rodapé da tabela acima, já calculamos o valor da potência aparente total de iluminação, tomadas e a potencia ativa das tomadas de uso específico.
Sobre a potência ativa total
Neste exemplo didático, vamos calcular a potência ativa total de uma instalação elétrica, e mostrar a aplicação do fator de potência.
Nossa instalação tem 660 VA de potência de iluminação, 7300 VA de potência de tomadas de uso geral (PTUG’s), e 12100 W de potência de tomadas de uso específico (PTUE’s).
Para calcular a potência ativa da iluminação e tomadas de uso geral, basta multiplicar a potência aparente pelo fator de potência correspondente.
Veja como ficou passo a passo, na imagem abaixo.
Já sabemos que a potência aparente da iluminação é 660 VA, e o fator de potência a ser adotado deve ser “1”, então vamos calcular.
para calcular a potência ativa, usei a fórmula do fator de potência, veja na imagem abaixo, como foi feito o cálculo passo a passo.
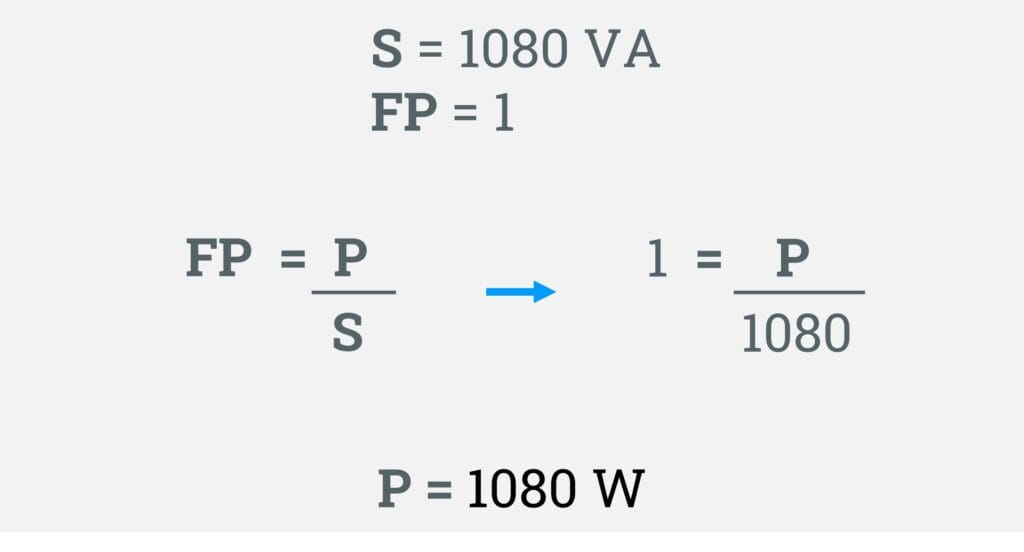
Fazendo os cálculos acima
Nós encontramos a potência ativa da iluminação no valor de 1080 W.
Agora, vamos calcular a potência ativa das tomadas de uso geral, conforme o exemplo anterior.
Já sabemos que a potência aparente das tomadas é 7300 VA, e o fator de potência a ser adotado neste caso, deve ser “0,8”, então vamos calcular.
Neste caso, vamos usar a mesma fórmula, conforme o exemplo anterior.
Agora, veja como ficou o cálculo passo a passo:
Para calcular a potência ativa das tomadas de uso geral, multiplicamos pelo fator de potência “0,8”, e encontramos a potência ativa de 5520 W.
Por último, temos as tomadas de uso específico, neste caso não é necessário aplicar fator de potência, pois este já tem uma potência ativa (12100 W).
Como nosso exemplo está pedindo a potência ativa total da instalação, nosso próximo passo é somar todas as potências ativa.
Veja como eu fiz passo a passo na imagem abaixo.
Ao realizar o somatório das potências ativas de iluminação, tomadas e tomadas de uso específicas, teremos a potência ativa total da instalação de 18700 W.
É em função da potência ativa total prevista para a residência que podemos determinar o tipo de fornecimento, a tensão de alimentação e o padrão de entrada.
Este foi apenas um exemplo da aplicação, usado em cálculos de projetos elétricos residenciais.
Mas se você possui uma empresa ou indústria, com muitos motores “pesados”, incluindo elevadores, deve se preocupar.
No próximo passo, vamos ensinar como fazer a correção do fator de potência, e porque ela é importante para a indústria, vamos la!
Como fazer a correção do fator de potência
Corrigir o fator de potência está intimamente relacionado com a indústria, devido a quantidade de carga gerada pelos motores e equipamentos indutivos.
A correção tem por objetivo reduzir o trânsito de energia reativa nas linhas de transmissão, subtransmissão e distribuição das concessionárias de eletricidade.
Mas o que pode causar o baixo fator de potência é o que vamos entender agora.
Baixo fator de potência
Fiz uma lista dos principais causas, veja!
- Transformadores operando a vazio ou subcarregados durante longos períodos de tempo.
- Motores operando em regime de baixo carregamento.
- Utilização de grande número de motores de baixa potência.
- Instalação de lâmpadas de descarga (fluorescentes, de vapor de mercúrio e de vapor de sódio) .
- Capacitores ligados nas instalações das unidades consumidoras horossazonais no período da madrugada.
Para que você possa aprender como calcular a correção do fator de potência, fizemos um exemplo passo a passo.
Exemplo de correção do fator de potência
Neste exemplo, nós iremos:
- Corrigir o fator de potência para 0,92.
- Determinar a potência reativa.
- Calcular o tamanho do capacitor.
Nosso exemplo, temos um motor elétrico de 10 CV de potência mecânica, cujo fator de potência é de 0,75 apresenta um rendimento de 90% e é alimentado a partir da rede de 220 Vef.
Qual seria o capacitor ideal que deve ser conectado em paralelo ao motor para corrigir o fator de potência para 0,92, segundo as normas brasileiras.
Para fazer os cálculos, nós iremos calcular a potência ativa, reativa e aparente do motor, então vamos lá!
Passo 1: Potência ativa do motor
Nosso primeiro passo é encontrar a potência ativa do motor, neste caso ela está informada em 10 CV.
Sabemos que 1 CV equivale a 736 W de potência, e que o nosso motor está operando com rendimento máximo de apenas 90%, veja os cálculos abaixo.
Ao finalizar os cálculos acima, encontrei o valor da potência ativa do motor, sendo 8177,8 W.
Agora nosso próximo passo é encontrar a potência aparente do motor.
Passo 2: Potência aparente do motor
No passo anterior, encontrei o valor da potência ativa, agora estamos em busca da potência aparente e da potência reativa do motor.
Como eu já tenho o valor da potência ativa e o valor do fator de potência do motor que foi informado no exemplo, fica mais fácil encontrá lo.
Então, para encontrar a potência aparente do motor, irei utilizar a fórmula básica, veja no cálculo abaixo.
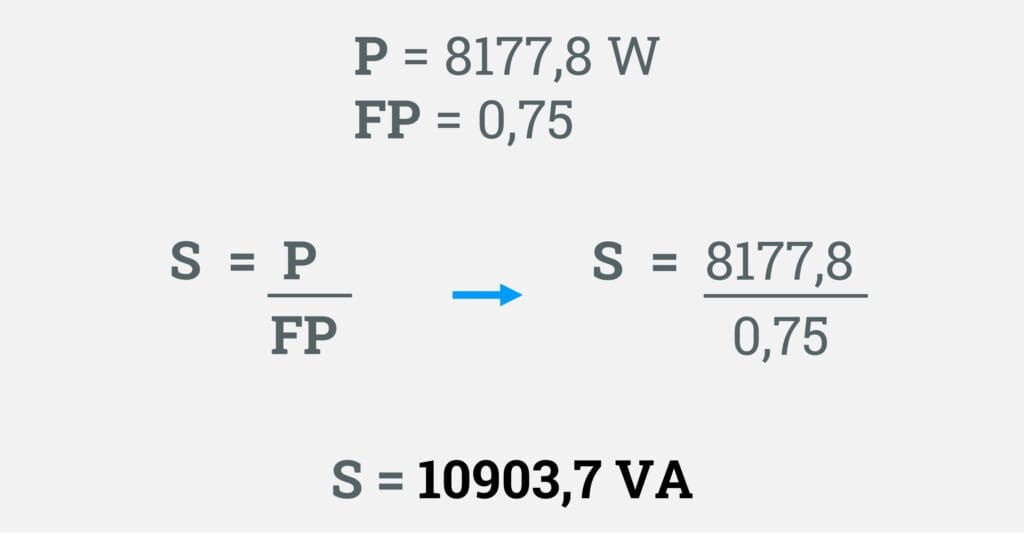
Fazendo a substituição dos valores na fórmula, encontrei a potência aparente do motor no valor de 10903,7 VA.
Agora nosso próximo passo deve ser encontrar a potência reativa.
Passo 3: Potência reativa do motor
Agora já temos o valor da potência ativa e a potência aparente, nos resta agora calcular o valor da potência reativa.
Nosso primeiro passo para calcular a potência reativa, foi calcular o ângulo do fator de potência (0,75), que foi dado no enunciado da questão.
Para encontrar o ângulo do fator de potência, basta calcular o inverso do cosseno do fator de potência que é 0,75 e encontramos o ângulo de 41,41°.
Depois de calcular o ângulo, basta inserir os valores na fórmula usada para calcular o fator de potência.
Fazendo a substituição dos valores na fórmula, encontrei a potência reativa do motor no valor de 7212,1 VAr.
Agora, veja a imagem abaixo do triângulo das potências com as respectivas potências calculadas do motor.
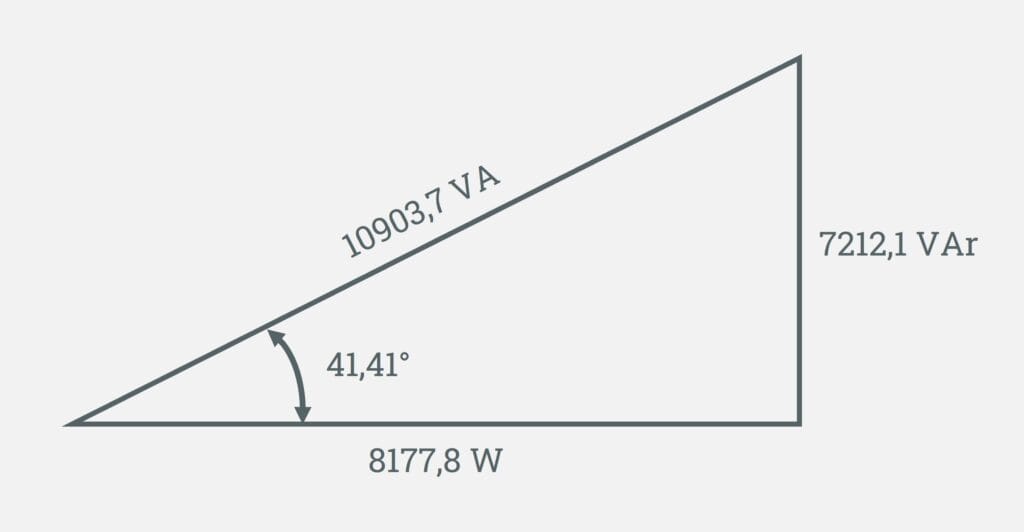
Nosso próximo passo é calcular a correção de 0,75 para o fator de potência desejado que é 0,92.
Passo 4: Calculando a potência aparente
A partir deste passo, iniciamos a correção do fator de potência atual de 0,75 para o fator desejado que é 0,92.
No Brasil as concessionárias de energia elétrica exigem uma eficiência mínima de 92% por parte dos clientes para que não seja cobrado a potência reativa (Kilo-Watt-Hora-Reativo).
Este limite pode variar dependendo do horário, sendo que, entre 6 e 24 h o fator deve ser no mínimo 0,92 para a energia e demanda de potência reativa indutiva fornecida.
Entre 24 e 6 h, o mínimo estabelecido é 0,92 para energia e demanda de potência reativa capacitiva recebida.
Além de gerar multas para a empresa, há um conjunto de consequências que podem ser geradas pelo baixo fator de potência, como:
- Incremento das perdas;
- Quedas e flutuações de tensão nos circuitos de distribuição;
- Sobrecarga nos equipamentos de manobra;
- Condutores aquecidos;
- Redução do aproveitamento da capacidade dos transformadores;
- Acréscimo na conta de energia elétrica devido a cobrança de excedentes.
Vimos que para alimentar uma carga de 8177,8 W com um fator de potência de 0,75 são necessários 10903,7 VA.
Para a mesma carga de 8177,8 W, mas com fator de potência igual a 0,92, vamos usar a mesma fórmula básica usada nos exemplos anteriores.
Como eu já tenho o valor da potência ativa e o valor do novo fator de potência do motor, basta inserir na fórmula, veja no cálculo abaixo.
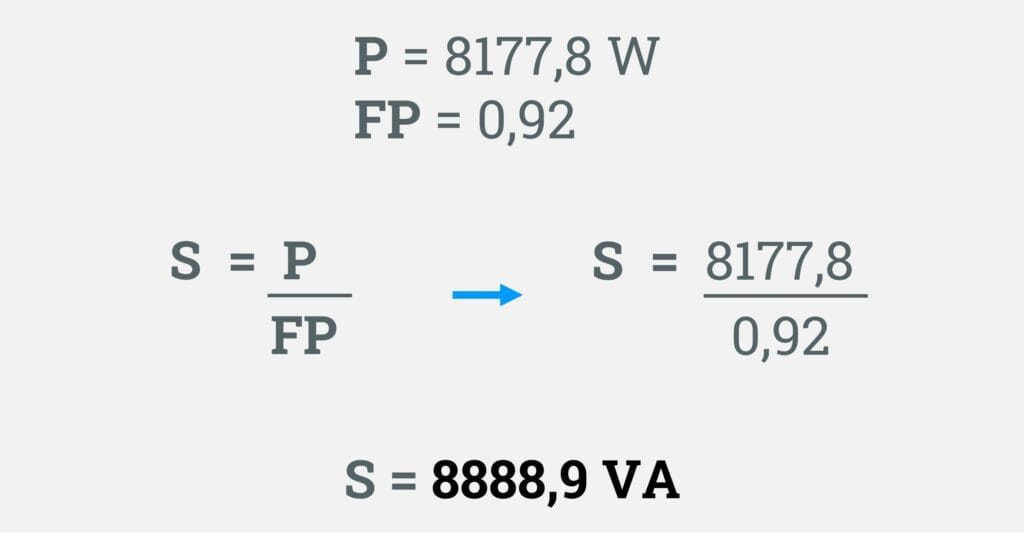
Fiz a substituição do valor da potência ativa de 8177,8 W, e do fator de potência desejado de 0,92.
Ao efetuar a divisão, encontrei o valor da potência aparente do motor no valor de 8888,9 VA.
Agora nosso próximo passo é encontrar o valor da potência reativa com base no novo fator de potência desejado.
Passo 5: Calculando a potência reativa
Agora já temos o valor da potência aparente, nos resta agora calcular o valor da potência reativa.
Nosso primeiro passo para calcular a potência reativa, foi calcular o ângulo do fator de potência desejado de 0,92, que foi dado no enunciado da questão.
Para encontrar o ângulo, basta calcular o inverso do cosseno do fator de potência que é 0,92, e encontramos o ângulo de 23,07°.
Depois de calcular o ângulo do fator de potência desejado, fiz os cálculos da potência reativa.
Usando a fórmula da potência reativa, fiz a substituição dos valores da potência aparente e o seno do ângulo.
Fazendo a substituição dos valores na fórmula, encontrei a potência reativa do motor no valor de 3483,2 VAr.
Agora, veja como ficou o triângulo das potências antes e depois da correção do fator de potência.
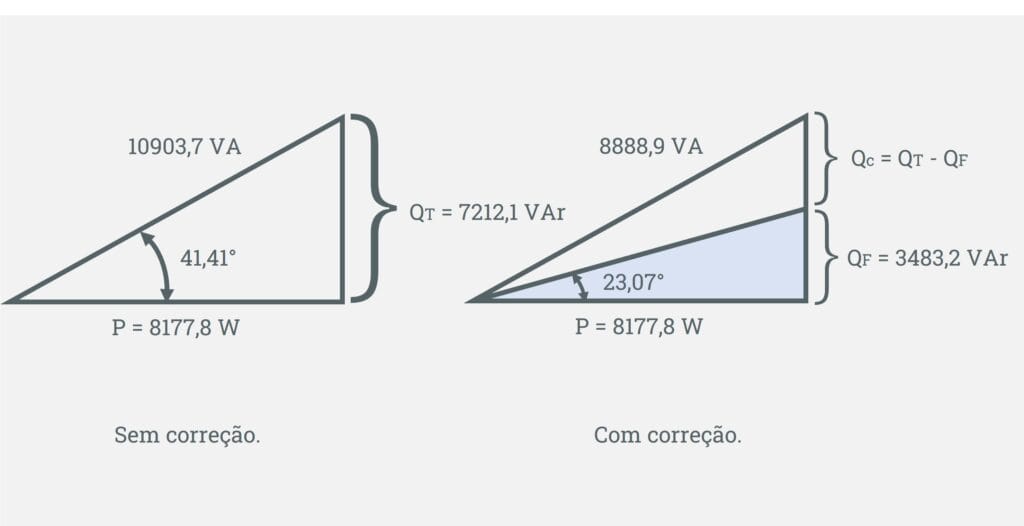
Na imagem acima, você deve ter percebido que houve uma redução significativa nos valores da potência reativa e aparente.
Ou seja, quando o fator de potência é corrigido conforme a legislação brasileira, a empresa passa a utilizar energia da forma mais correta e econômica.
Por isso, fiz uma lista das principais vantagens esperadas após a correção, veja abaixo:
- Desaparece o acréscimo cobrado nas contas de energia elétrica.
- Melhora o aproveitamento da energia elétrica para geração de trabalho útil.
- Diminuem as variações de tensão (oscilações).
- Melhora o aproveitamento dos equipamentos com menos consumo.
- Aumenta a vida útil dos equipamentos.
- Os condutores tornam-se menos aquecidos, diminuindo as perdas de energia elétrica na instalação.
- Devido à liberação de carga, a capacidade dos transformadores alcança melhor aproveitamento.
Nosso próximo passo agora é calcular a quantidade de potência reativa excedente para dimensionar corretamente o capacitor.
Passo 6: Escolha do capacitor
Ao calcular a correção do fator de potência, nosso objetivo é reduzir a quantidade de potência reativa gerada pelo motor.
Observando o triângulo das potências acima, podemos verificar que a potência reativa sem a correção é 7212,1 VAr e após a correção do fator de potência ele deve ser de 3483,2 VAr.
Fazendo o seguinte cálculo, a diminuição entre a potência reativa anterior e a potência reativa desejada, encontramos o excedente de potência reativa que deve ser eliminado.
É importante saber que existem várias maneiras de corrigir um baixo fator de potência, por exemplo:
- O dimensionamento correto de motores e equipamentos.
- A seleção, utilização e operação correta de motores e equipamentos elétricos em geral.
- A utilização permanente de reatores de alto fator de potência.
- A instalação de capacitores ou banco de capacitores onde for necessário (de preferência próximo da carga).
- A instalação de motores síncronos em paralelo com a carga.
Uma das formas mais utilizadas para resolver esse tipo de problema e corrigir o fator de potência, é armazenando parte da potência reativa do motor.
Ou seja, para corrigir o problema do nosso motor, o ideal seria instalar capacitores para correção do fator de potência.
Desta forma, podemos elevar o fator de potência atual de 75% para 92% de eficiência, em conformidade com as leis brasileiras, e evitando multas.
Isso significa que devemos armazenar 3728,9 VAr de potência reativa para conseguir manter um fator desejado de 0,92.
Qual seria o tamanho do capacitor ideal para armazenar essa potência reativa e corrigir o fator de potência?
Passo 7: Dimensionando o capacitor ideal
No passo anterior você já aprendeu como calcular a potência reativa que será armazenada no capacitor do nosso motor.
O nosso capacitor deve ser dimensionado para armazenar 3728,9 VAr de potência reativa, e possui uma Vef de 220 V e frequência de 60 Hz conforme o enunciado da questão.
Para dimensionar o tamanho ideal do capacitor e corrigir para o fator de potência desejado de 0,92, vamos usar a fórmula abaixo.
Onde:
- C = Capacitância;
- Q = Potência reativa;
- f = Frequência;
- V = Tensão;
Sei que pode parecer um pouco confuso essa fórmula inicial acima para calcular o capacitor, mas resumindo, a expressão ficará da seguinte forma abaixo.
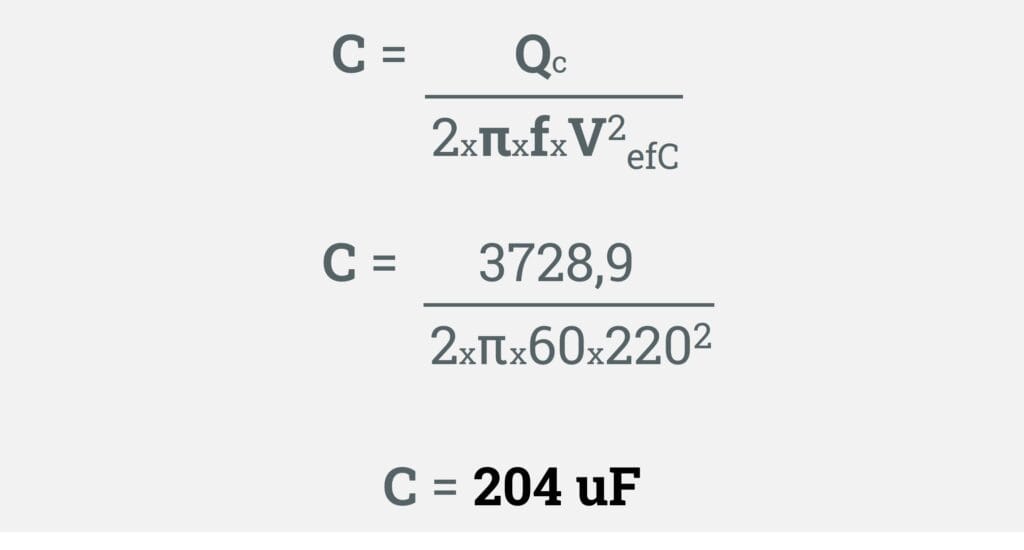
De posse dos valores obtidos, fiz a substituição dos seguintes valores na fórmula conforme calculado anteriormente e conforme enunciado na questão.
Ao efetuar os cálculos acima, podemos concluir que o capacitor ideal para armazenar 3728,9 VAr de potência reativa, deve ter um tamanho ideal de 204 μF.
Resumindo, para alimentar uma carga de 8177,8 W com fator de potência de 0,75 são necessários 10903,7 VA.
Para a mesma carga de 8177,8 W, mas com o fator corrigido igual a 0,92, são necessários apenas 8888,9 VA.
